Can Math be Magical? A Mathemagician Shows How

By Bibi Hanselman and Bryan Shi

On October 16, the Science Center lobby buzzed with a lively atmosphere, packed with students enjoying snacks as they huddled around several of their peers and watched them pull off a variety of card tricks. But among these performers was the true star of the show: Dr. Arthur Benjamin, a Professor of Mathematics at Harvey Mudd College who’s better known for performing mathemagics — his fusion of math and magic — for audiences around the world. He has appeared on the Colbert Report, Today, and NPR, and is profiled in The New York Times, among other prominent publications. This time, he was visiting Amherst to give his signature show. As the time drew closer to 4:00 pm, the crowd — composed of math enthusiasts and casual listeners alike — poured into Lipton Lecture Hall, eagerly awaiting Dr. Benjamin’s mathemagical performance.

Part 1: Math or Magic?

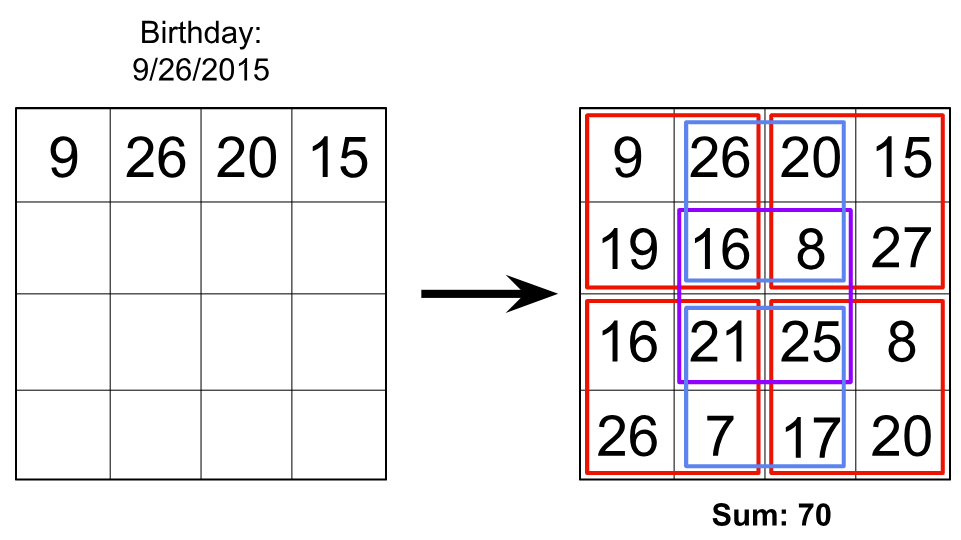
To open the show, Dr. Benjamin gripped the audience with a perplexing magic trick involving an invisible deck of cards. Soon, the mathemagician turned to tricks involving math, showcasing his distinctive mental math capabilities. He left volunteers stunned as he raced against their calculators to compute the squares of two-digit numbers. Not only was he able to multiply two-digit numbers faster, but he could also beat them at three-digit squares with relative ease. He left the audience even more astounded by crossing into magical territory with his spin on the classic magic square. This entailed inserting a volunteer’s birthday into the first row of a 4×4 grid and, within seconds, conjuring a solution in which all the rows, columns, diagonals, and smaller squares summed to the same number.

From plucking missing digits from unknown products to guessing the day of the week of birthdays, Dr. Benjamin demonstrated his mathematical acuity and imbued his problem-solving with a magical touch. He created a sense of bewilderment that captivated the crowd from start to finish, showcasing his top-notch performative skills as both a proficient human calculator and an apt magician.

Trick after trick, Dr. Benjamin was consistently met with enthusiastic applause, and there appeared no reason for him to stop. But 15 minutes in, he took a sudden turn in his performance, and it was to everyone’s unexpected delight: unlike most magicians, Dr. Benjamin offered to reveal the secrets behind his mathemagics, opening up to a Q&A style discussion for the remaining 45 minutes of the show. “For an audience such as this one, I actually prefer to break the magician’s rule,” he explained. Aside from his card trick at the beginning, which he refused to explain — lest he be kicked out of “the magic castle” — Dr. Benjamin was receptive to the audience’s burning questions, jumping almost immediately into the mystery of the birthday magic square.

Part 2: Secrets of the Square

As Dr. Benjamin redrew his magic square on a fresh sheet of easel paper, the illusion of inexplicable magic crumbled, giving way to a relatively simple mental math exercise. His approach began with placing the two middle numbers of the birthday in the empty corners to guarantee the final surprise of his trick (though he noted not to actually write down both at first, as that would spoil the magic). From that, Dr. Benjamin described his clever strategy to complete the rest of the square, starting with a critical moment: taking the third number, 20, adding 1, and placing it in the space diagonally adjacent to the bottom-left corner. Now, in “the easiest sudoku puzzle ever,” you can simply fill in the columns, rows, diagonals, and inner squares, beginning with the diagonal where the 21 was just placed. If you have a single empty square left, you take the sum obtained from the first row and subtract each number already filled in. That way, every column, row, diagonal, and inner square will share the same sum (in Dr. Benjamin’s example, 70), as mandated by the magic square. And as it turned out, the choice to add 1 to 20 was crucial. Had Dr. Benjamin used 20, he explained, the remaining numbers would’ve just worked out to be the same as the first four. Not magical at all! Adding this slight modification beforehand introduced variation in the remaining numbers while minimizing the complexity of the mental math, making Dr. Benjamin’s magical stunt appear all the more convincing.

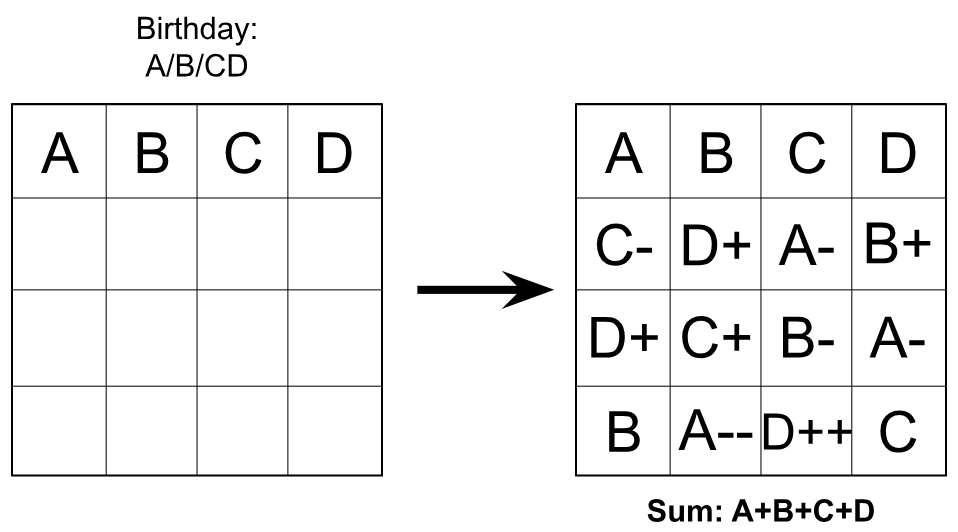
Although the audience painlessly followed and understood Dr. Benjamin’s reasoning, he wasn’t satisfied with that explanation alone. He spoke of “the math professor” within him, seeking to dispel any lingering magic by more rigorously proving that the magic square would work out for any choice of numbers in the first row, which he represented with A, B, C, and D. It was this representation of the square, he noted, that allowed him to respond to any birthday and produce the correct magic square on the spot.

Part 3: Secrets of the Square (the Other Kind)

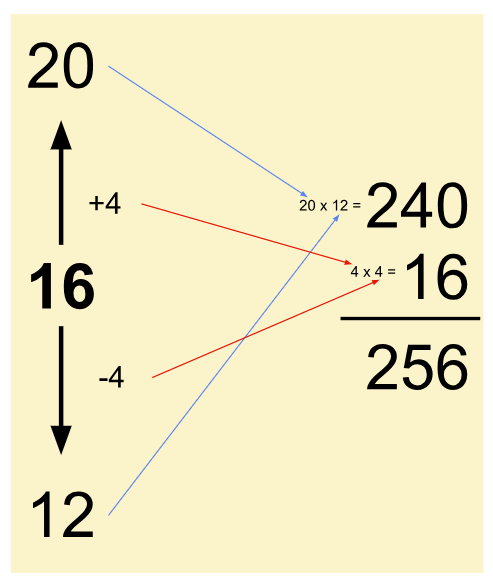
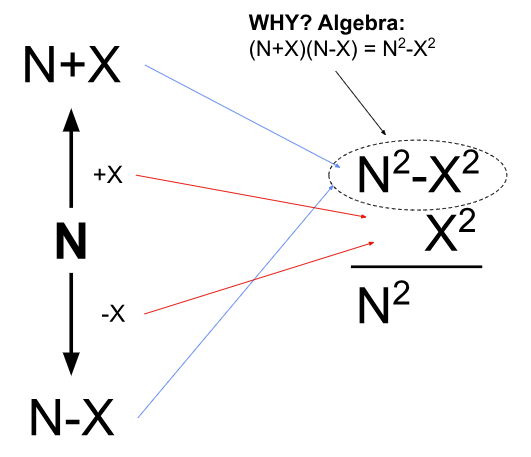
Dr. Benjamin’s desire to equip the audience with his mathemagical tools, and to generally demystify mental math, turned out to be a central theme of his demonstrations, which carried on as he presented his method to quickly square numbers. Through a series of examples, he broke down the multiplication process into more digestible steps. Say you want to compute the square of any number N — that is, N². From N, first add a number X to get a more easily multipliable number (N+X) — usually a multiple of 10. Indeed, Dr. Benjamin adorned the 0’s with smiley faces to remind the audience that multiplying by multiples of 10 isn’t as bad as one might think. Next, subtract X from the original number: (N-X). Now, to get N², multiply the two numbers (N+X)(N-X), and finally add X². Algebraically, the process can be shown by (N+X)(N-X) + X² = N² – X² + X² = N²: a proof that the math professor in Dr. Benjamin did not discount. Since adding X to N results in an easily multipliable number and X² should be relatively small, the math becomes much easier to do mentally — easy enough, in fact, for Dr. Benjamin to invite listeners to join in and square some two-digit numbers for themselves. 

Unfortunately, for three- and four-digit numbers, the math becomes complicated quickly — even for a whiz like Dr. Benjamin. This is because it demands remembering many large numbers while performing multiple layers of multiplication and addition. To easily store these numbers in memory, Dr. Benjamin introduced the audience to the major system, which converts numbers into consonants. After converting each digit of a number into a consonant, he then inserts vowels between the consonants to create a recognizable word. For instance, if 1 corresponds to T and 5 corresponds to L, the consonant conversion of 15 would be “TL.” Adding some vowels results in the word “TooL.” This mnemonic system becomes increasingly useful as calculations begin to involve larger numbers. Instead of remembering 192,303 while doing other operations, all you would need to keep in mind is the phrase “TaP NuM SaM!”

At last, all the foundations were laid for the mathemagician’s grand finale in which he would square a five-digit number all in his head. He’d promised this early on, but it didn’t play out so traditionally. Unlike his mathemagical tricks from earlier, Dr. Benjamin would not cast himself as an ordinary magician. Instead, to ensure that the audience would identify with his shortcuts, he voiced his live computational process out loud rather than hiding it. The audience caught on and mentally joined in with him, following a rapid but intelligible stream of calculations that synthesized seemingly unrelated mental math tricks to arrive at a singular satisfying result. Importantly, there was still the flair of magic that set the performance in course from the beginning. Dr. Benjamin’s mental math capabilities remained impressive despite all the arithmetic shortcuts he’d unveiled during the hour. 

As he reached his memory’s limits, Dr. Benjamin blurted out his final calculations and scrawled the final digits of his answer on the easel. 1,356,227,929, it read. The hall burst into applause.