
Tell us a bit about yourself; what life experiences influenced you to write a senior thesis?
I’ve always liked math. I think my parents did a good job of encouraging that when I was young, and I got lucky and had a number of good math teachers who were very encouraging. I had a kind of weird math experience; I took 9th grade and half of 10th grade off from doing it, so I was kind of behind. Between January in 10th grade and the start of 11th grade, I learned algebra 2 at a community college and pre-calculus at an online summer school. It was terrible, I didn’t really understand the material, and trigonometry was so boring that I decided I would be a political science major. Then I took calculus. The very notion of a limit blew my mind so much that I became practically obsessed. I started watching Khan Academy videos for fun and kind of taught myself the whole curriculum for my Calc AB class. By the end of my junior year, I knew math was for me, and by the time I got to college, I had realized I would never be satisfied with the amount of math I knew. I read about senior theses on Amherst’s website and couldn’t wait to do one and go off to grad school.
Is your thesis research related to any prior research experiences?
Strictly speaking, no. That being said, I had a good idea about the kind of math I liked starting the summer before college when I found YouTube videos on topology and differential geometry. So my summer research projects after my first and second year of college were influenced by my desire to explore those areas more. [My projects] helped clarify what I did and didn’t like and introduced me to the rabbit hole I would follow that led to my thesis topic.
Can you please talk about the research you’re doing for your senior thesis?
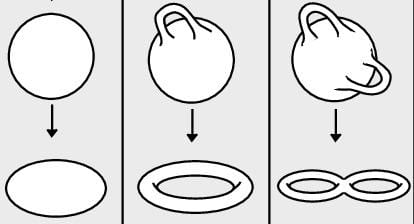
My thesis is primarily interested in studying four-dimensional shapes, called manifolds, using calculus/analysis and mathematical physics (there are plenty of groups, rings, and fields that go into it, too). The most basic thing topologists are interested in is studying “holes” in higher dimensional spaces to tell them apart – think of the difference between a torus and a pretzel, for example, one vs. three holes. One can generalize this idea to solve a lot of really interesting high-dimensional problems. My thesis concerns studying a measure of “complexity” to holes in three- and four-dimensional manifolds. Once you have the background, it’s pretty easy to define and very, very hard to compute. This [type of work] has been a pretty big subject of research for the last 40 years. My thesis specifically focuses on studying the complexity of holes in four-manifolds that “look like” three-manifolds, since studying complexity in three-manifolds is much easier. My goal was to lift information from three dimensions to four. I was…kind of successful.
What kinds of responsibilities do you have when conducting your research?
The fun thing about math is there’s no physical component of research. That meant that the bulk of my thesis consisted of being confronted with a stack of very difficult textbooks and research papers and trying to decipher them. Sometimes these were on the suggestion of my advisor, and sometimes I’d see something referenced in a research paper and go down a rabbit hole trying to figure out if the idea could be of any use. It wasn’t three-quarters of the time, but that’s how math research goes.
What does the schedule of a thesis student look like?
I met with my advisor once a week. During our meetings, I’d talk with him about what I was doing, which was usually one of two things: trying to digest a difficult piece of math that I’d thought could be useful or playing around with a research strategy or a lemma and trying to apply whatever math I’d recently learned. He’d read whatever I wrote that week, either an attempt at proving a new lemma or an exposition of what I’d read. Writing expositions was very useful in clarifying my understanding and also gave me material to turn into my written thesis when the time came. It also made me a much better writer. After we talked about [my work], I’d either say, “this is my plan for the next week: I’m gonna try to prove this little conjecture I made,” or “I’m stumped, this didn’t work, do you have any suggestions for things I could try or read to figure out how to move forward?” Rinse and repeat for a year, and I had a thesis.
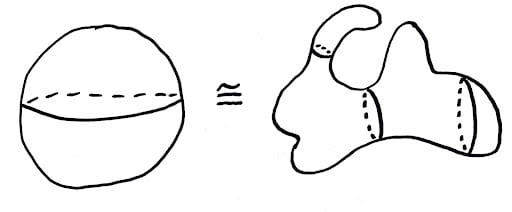
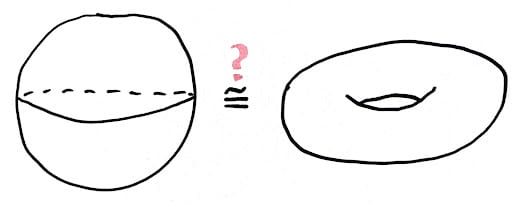
Figure 2: Images used in thesis presentation. Photos courtesy of Audrey Rosevear.
In what ways does your research play into the “bigger picture” that you find meaningful?
A very weird part of topology is that four-dimensional manifolds are the hardest in some sense. Weirdly enough, certain problems become much easier once you get to higher dimensions. It’s not entirely true to say that we know nothing about four dimensions, but it’s not too far off. On the other hand, three dimensions are this huge exploding field where a lot of progress has been made (if you’ve heard of the million-dollar Poincaré Conjecture, the proof of that was like a pretty big deal). So a lot of topologists are trying to leverage these four-dimensional ideas in four-dimensions to see if we can get any traction. I stumbled on a big conjecture in my thesis made 20 years ago and saw no progress. I gave a partial proof of a special case. It’s not much, but this is, as far as I can tell, the first time anyone has made any progress on it. I kind of got lucky as I used techniques that have popped up in the last three years. This conjecture, and ones like it, represent a potential way to crack the mysteries of four dimensions using what we know in three dimensions.
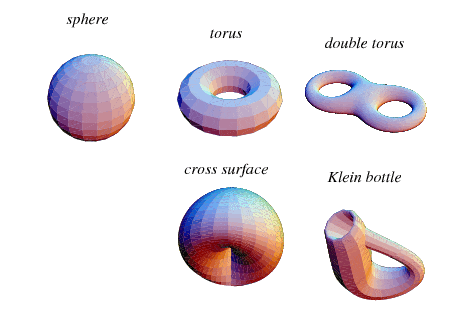
What advice do you have for students interested in writing a thesis?
Your thesis will probably be the first time in your education you’re given a big enough project that you have room to fall flat on your face, and that’s okay! I had at least three times in my thesis when my entire research strategy turned out to be bunk, and I went back to square one. That’s how it goes when your professors do research too, but you only ever see the final product and don’t know how many times they failed in getting there. Find an advisor that will encourage you to get back up when these things happen. It’ll be hard to avoid getting demoralized at times. Take a break, ignore your thesis for a few days, and don’t try to fix the problem just yet [when you come back]. Go find a paper to read. Remind yourself why your thesis problem is exciting and keep exploring until you are struck with an idea of how to move forward. Your thesis is shorter than it feels like it will be at the beginning. You may not finish everything you’d hoped to do, and that’s okay! I didn’t. Maybe I’ll finish in grad school; maybe I won’t. Either way, I sure as hell learned a lot.
You must be logged in to post a comment.